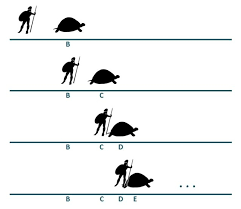
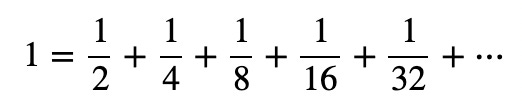Achilles and the Tortoise
Achilles, the hero of the Trojan War and protagonist of the Iliad, is in a race with a tortoise. Achilles gives the tortoise a head start – let's say 1/2 mile. After some time, Achilles runs 1/2 mile, catching up to where the tortoise initially started. In that time, the tortoise has moved a small distance – let's say 1/4 mile. Next, Achilles covers that distance, but the tortoise has still advanced, albeit a much smaller distance.
This is one of Zeno's paradoxes: Achilles never seems to catch up to the tortoise. Every time Achilles catches up to the tortoise's last position, the tortoise has moved just a little bit further. The gap between the two gets smaller and smaller, but it always exists.
Aristotle wrote about Zeno's paradoxes in his Physics. (Much later, Lewis Carroll expands on this particular paradox in his What the Tortoise Said to Achilles.)
In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. – Aristotle, Physics
Of course, Achilles can catch up to the tortoise. Zeno knew this but didn't have the mathematical tools (i.e., infinitesimal calculus) to prove otherwise. At the root of the solution to the paradox is that an infinite series can have a finite sum. Using the example above, Achilles needs to first cover 1/2 mile, then 1/4 mile. Now the tortoise has moved 1/8 mile. We say that this series converges.
I like Zeno's paradox because it shows our intuition about infinite quantities but also our trouble with formally reasoning with it. I wrote about some other paradoxes like this in Strange Loops (and more contained in the book I Am a Strange Loop by Douglas Hofstadter).