Braess's paradox
In 1990, the New York City Transporation Commissioner closed 42nd Street for Earth Day. Everyone expected that closing a major cross-town artery would cause historic traffic jams. Instead, traffic flow improved.
One of Seoul's busiest freeways, the Cheonggyecheon Freeway, was built over the Cheonggyecheon River and ran through the heart of the city. It carried 168,000 cars per day. In an effort to restore the river, the city demolished it and built a 5-mile public park. Travel times improved, and traffic volume stayed roughly the same.
The counterintuitive result is called Braess's paradox:
Adding a new road to a traffic network could make overall travel times longer
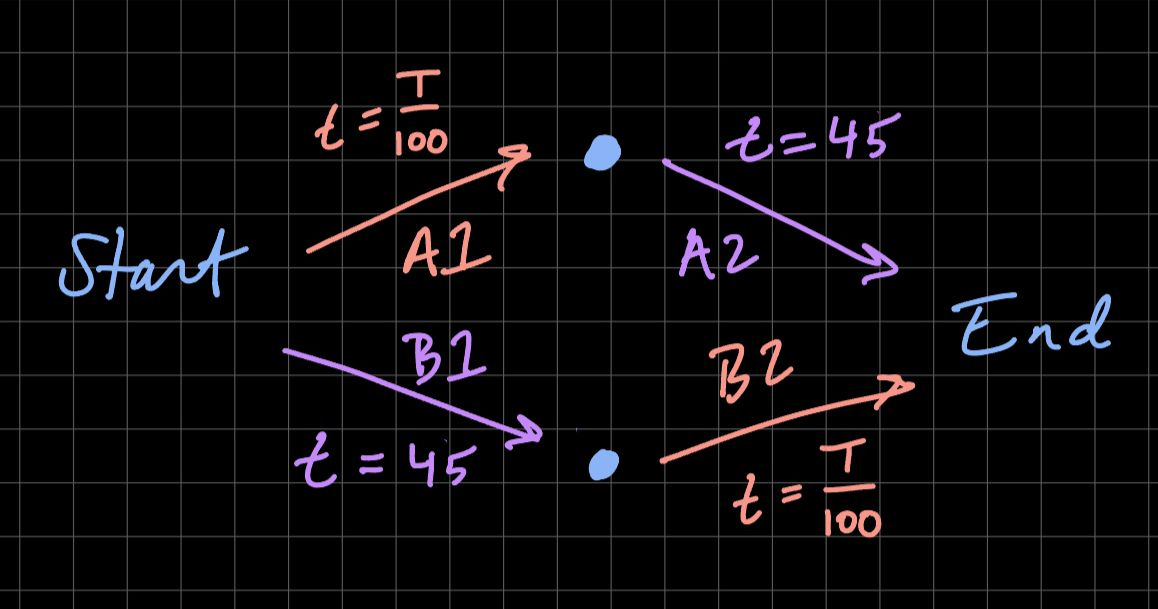
Suppose there are 4000 drivers going from start to end. They can initially choose to take routes: A1 -> A2 or B1 -> B2. The travel time for B1 and A2 is a constant 45 minutes (imagine a large highway with many lanes). The travel times for A1 and B2 is dependent on the number of cars on the road T, let's say T/100 minutes.
The equilibrium here is that 2000 drivers pick A1 -> A2 and 2000 drivers pick B1 -> B2. That's 2000/100 + 45 = 65 minutes per driver.
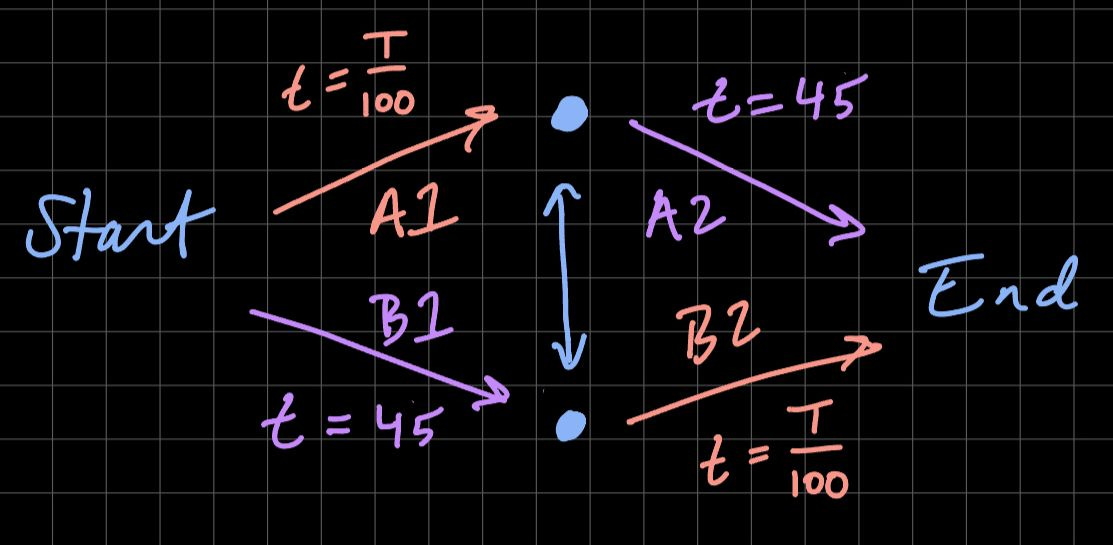
Now suppose there's a zero-minute road added that connects the midpoints.
Now, every rational driver will start with A1 since it is, in the worst case, only 40 minutes compared to B1. Once at the midpoint, the rational driver will take the zero-minute road and then choose B2, using the same logic from the first leg of the trip. Each driver's total trip is now 4000/100 + 4000/10 = 80 minutes!
If every driver agreed not to use the zero-cost interchange, then travel times would decrease by 15 minutes. However, no single driver would rationally do that.
You might notice that Braess's paradox is not special but rather a Nash Equilibrium that isn't Pareto optimal. This is true; however, the Pareto impairment comes from adding a new link to the network, which is counterintuitive.
If you're looking for a more mathematical treatment, check out this chapter in Networks, Crowds, and Markets.